6-Convolutional-Neural-Network-(CNN)
机器视觉精品课程-卷积神经网络部分
© Xiaolong Wang 3180105098@zju.edu.cn
授课内容
- 基础概念回顾与拓展、梯度反向传播、交叉损失熵、Softmax回归、卷积神经网络
- 对上节课内容有问题的先提出进行讲解或者为本节课内容
- nn:neural network
- Sequential:顺序容器
- Linear(m,n):m个输入,n个输出的1层神经网络,其中n也可以代表这一层有多少个神经元
import numpy as np
import torch
def step_func(x): # 参数x可以接受numpy数组
y = x >= 0 # y是布尔型数组
return y.type(torch.int)
# 定义单个神经元 2输入
net = torch.nn.Sequential(torch.nn.Linear(2,1))
# 定义权重
w = torch.tensor([1,1]).type(torch.float32)
b = -2
net[0].weight.data = w.reshape(net[0].weight.shape)
net[0].bias.data.fill_(b)
# 验证输出
x = torch.tensor([1.0, 1.0]).type(torch.float32)
print('The result of 1 and 1 is', step_func(net.forward(x)).item())
x = torch.tensor([0, 1.0]).type(torch.float32)
print('The result of 1 and 1 is', step_func(net.forward(x)).item())
x = torch.tensor([0, 0]).type(torch.float32)
print('The result of 1 and 1 is', step_func(net.forward(x)).item())
torch.matmul(x, w) + b
The result of 1 and 1 is 1
The result of 1 and 1 is 0
The result of 1 and 1 is 0
tensor(-2.)
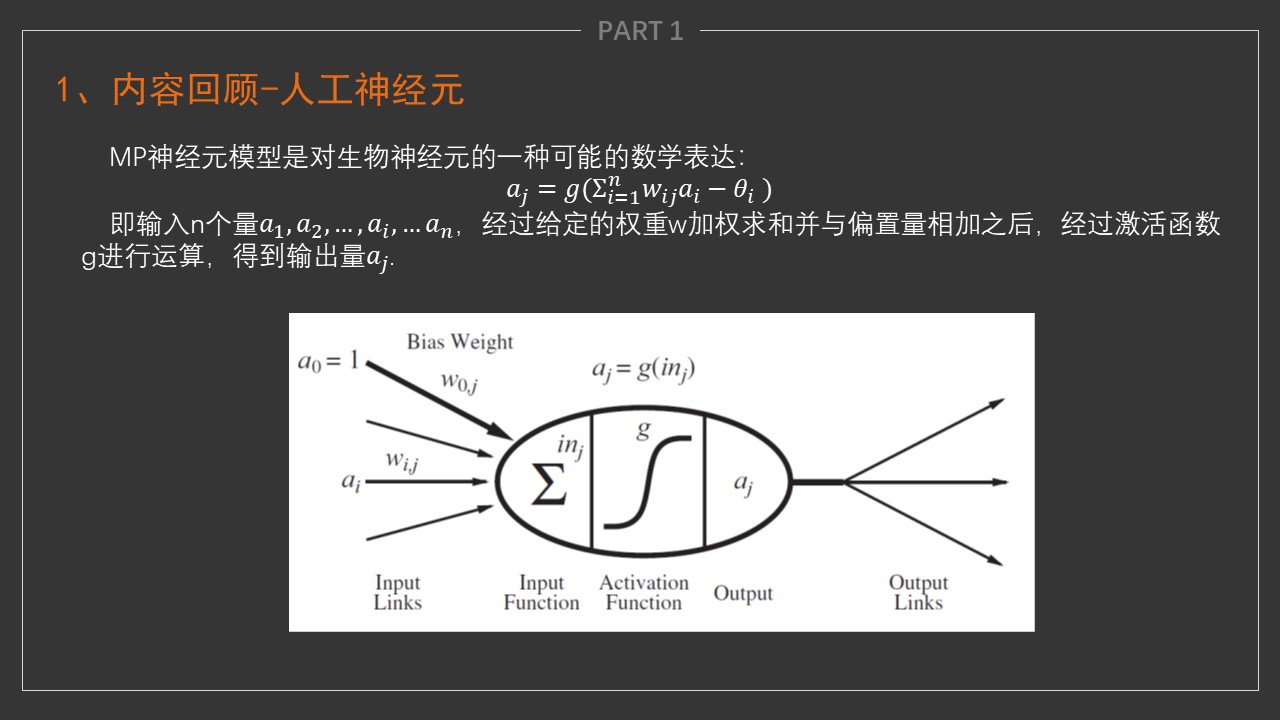
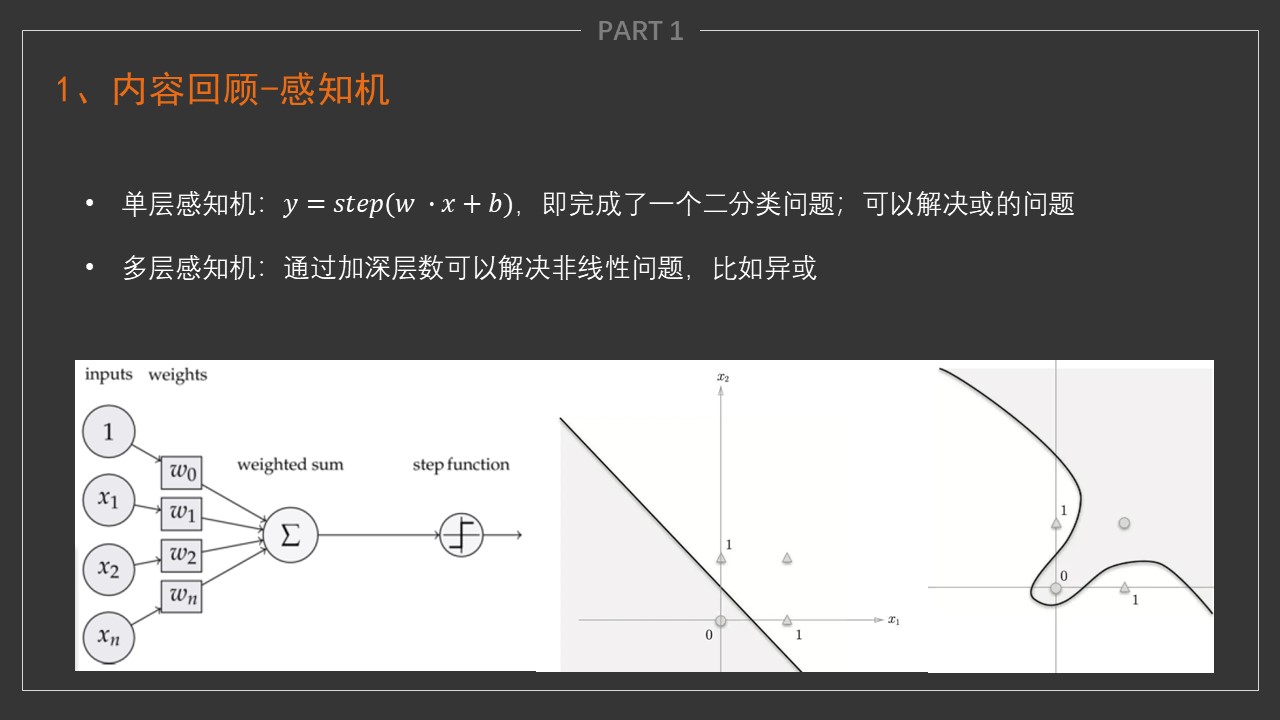
- 神经网络是基于感知机的扩展,而DNN(deep-neural-networks)可以理解为有很多隐藏层的神经网络。多层神经网络和深度神经网络DNN其实也是指的一个东西,DNN有时也叫做多层感知机(Multi-Layer perceptron,MLP)。
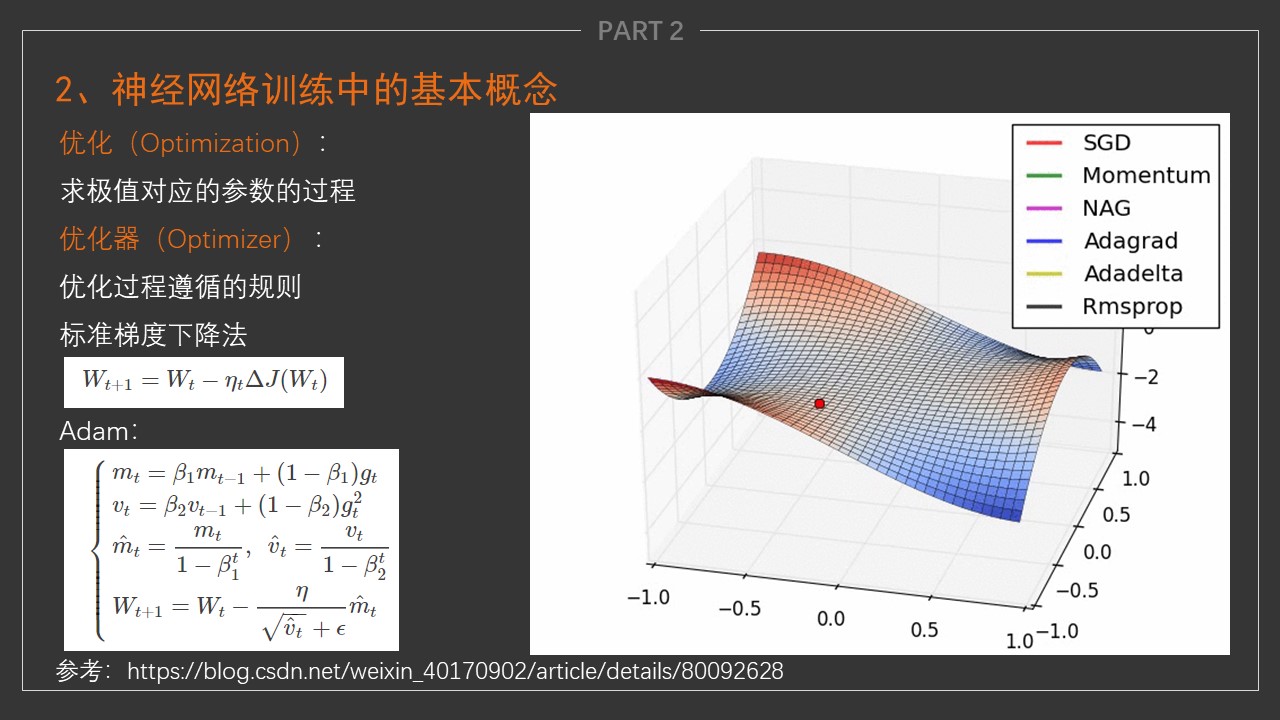
梯度下降
- 用到一种名为梯度下降(gradient descent)的方法,这种方法几乎可以优化所有深度学习模型。
- 它通过不断地在损失函数递减的方向上更新参数来降低误差。
-
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值)关于模型参数的导数(在这里也可以称为梯度)。
- 我们用下面的数学公式来表示这一更新过程(\(\partial\)表示偏导数):
总结一下,算法的步骤如下:
(1)初始化模型参数的值,如随机初始化;
(2)利用数据集在负梯度的方向上更新参数,并不断迭代这一步骤。
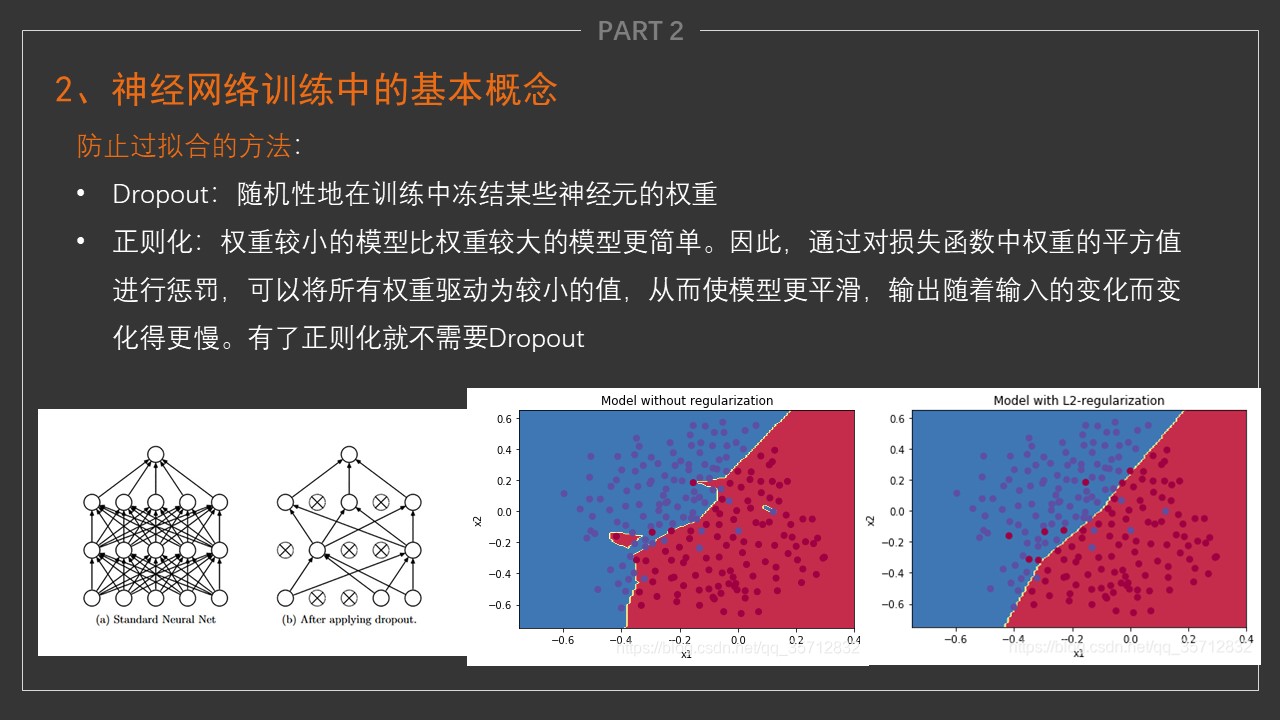
Dropout
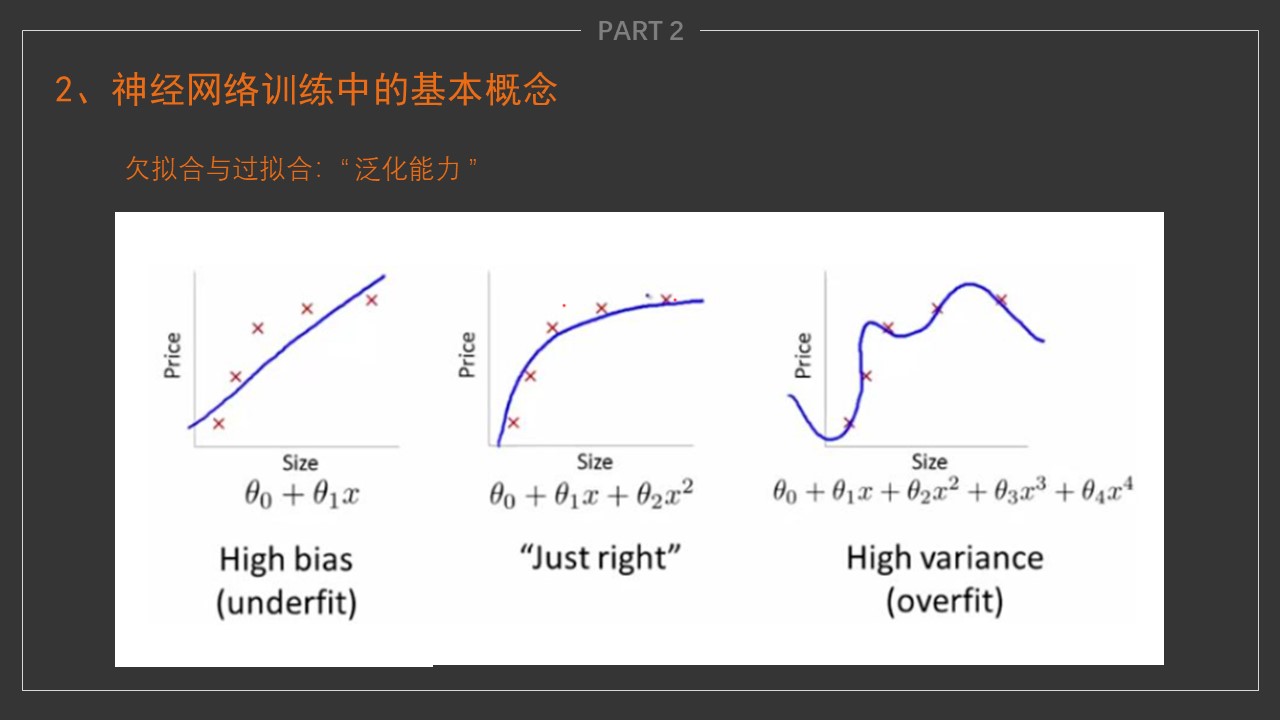
- 过拟合相当于一条道走到黑,加入dropout,它强迫一个神经单元,和随机挑选出来的其他神经单元共同工作,达到好的效果。消除减弱了神经元节点间的联合适应性,增强了泛化能力。
- 过拟合中无限逼近某个噪声点,dropout将它从这个过程中拉出来
正则化
- J(θ)+λR(w)
- torchvision 中的 transforms 模块可以针对每张图像进行预处理操作
- ILLUSTRATION OF TRANSFORMS
from torchvision import transforms # 图像变换、数据预处理
import cv2
import matplotlib.pyplot as plt
#Compose是一个容器,传入的参数是列表,ToTensor(),类型变换,Normalize是数据标准化,去均值,除标准差
# transforms.ToTensor() 把取值[0, 255]的PIL图像形状为[H,W,C]转换为形状[C,H,W] 取值范围[0,1.0]的张量
# transforms.RandomRotation(degrees=(0, 180))
transform = transforms.Compose([transforms.ToTensor(),transforms.RandomPerspective(distortion_scale=0.6, p=1.0),transforms.RandomRotation(degrees=(0, 180))])
cat_bgr = cv2.imread(r'./https://haodong-li.com/zju/assets/img/vision_2022/cat.jpg')
cat_rgb = cv2.cvtColor(cat_bgr, cv2.COLOR_BGR2RGB)
plt.subplot(1,2,1)
plt.imshow(cat_rgb)
cat_trans = transform(cat_rgb)
plt.subplot(1,2,2)
plt.imshow(cat_trans.numpy().transpose((1,2,0)))
<matplotlib.image.AxesImage at 0x1c310343c40>

梯度反向传播(Back Propagation,BP)
- 参考链接:Back Propagation(梯度反向传播)实例讲解
- 为什么要求梯度?
- 求关于谁的梯度?
损失函数
均方误差 MSE(mean squared error)
在我们开始考虑如何用模型拟合(fit)数据之前,我们需要确定一个拟合程度的度量。
- 损失函数(loss function)能够量化目标的实际值与预测值之间的差距。
- 通常我们会选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。
- 回归问题中最常用的损失函数是平方误差函数。
- 当样本\(i\)的预测值为\(\hat{y}^{(i)}\),其相应的真实标签为\(y^{(i)}\)时, 平方误差可以定义为以下公式:
- 为了度量模型在整个数据集上的质量,我们需计算在训练集\(n\)个样本上的损失均值(也等价于求和)。
- 在训练模型时,我们希望寻找一组参数(\(\mathbf{w}^*, b^*\)),这组参数能最小化在所有训练样本上的总损失。如下式:
梯度下降法(SGD, Stochastic Gradient Descent)
\(w^{+}=w-\eta \cdot \frac{\partial L}{\partial w}\)
理论依据
自动求导/数值求导
\(\frac{\partial f(x)}{\partial x}=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
链式法则
\(y=f(u), u=g(x) \quad \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u} \frac{\partial u}{\partial x}\)
举例
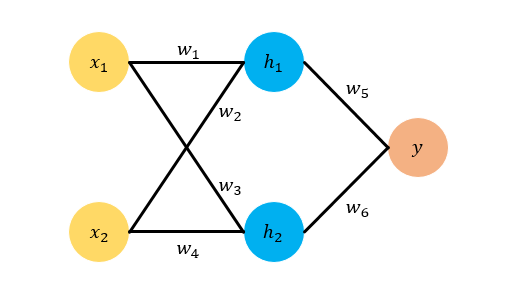
- 误差 \(E=\frac{1}{2}(y-t)^{2}\)
- 更新\(w_{5}\) \(\frac{\partial E}{\partial w_{5}}=\frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial w_{5}} \\ w_{5}^{+}=w_{5}-\eta \cdot \frac{\partial E}{\partial w_{5}}\)
- 更新\(w_{1}\) \(\frac{\partial E}{\partial w_{1}}=\frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial h_{1}} \cdot \frac{\partial h_{1}}{\partial w_{1}} \\ w_{1}^{+}=w_{1}-\eta \cdot \frac{\partial E}{\partial w_{1}}\)
import numpy as np
import torch
# 定义单个神经元 2输入
net = torch.nn.Sequential(torch.nn.Linear(2,2),torch.nn.Linear(2,1))
# 定义权重
net[0].weight.data = torch.tensor([1,2,3,4]).type(torch.float32).reshape(net[0].weight.shape)
net[1].weight.data = torch.tensor([0.5,0.6]).type(torch.float32).reshape(net[1].weight.shape)
net[0].bias.data.fill_(0)
net[1].bias.data.fill_(0)
x = torch.tensor([1.0, 0.5]).type(torch.float32)
net(x)
tensor([4.], grad_fn=<AddBackward0>)
# 数值求导举例
# 定义权重
net[0].weight.data = torch.tensor([0.5,1.5,2.3,3]).type(torch.float32).reshape(net[0].weight.shape)
net[1].weight.data = torch.tensor([1,1]).type(torch.float32).reshape(net[1].weight.shape)
# y1 = 0.5*(4-net(x).item())**2
y1 = net(x).item()
dx = 0.001
net[0].weight.data = torch.tensor([0.5,1.5,2.3,3]).type(torch.float32).reshape(net[0].weight.shape)
net[1].weight.data = torch.tensor([1+dx,1]).type(torch.float32).reshape(net[1].weight.shape)
# y2 = 0.5*(4-net(x).item())**2
y2 = net(x).item()
(y2-y1)/dx
1.2497901916503906
# 数值求导举例 y = x^T * x
import torch
x = torch.arange(4.0)
x.requires_grad_(True)
y = 2 * torch.dot(x, x)
y.backward()
x.grad,x.grad == 4 * x
(tensor([ 0., 4., 8., 12.]), tensor([True, True, True, True]))
Softmax激活函数
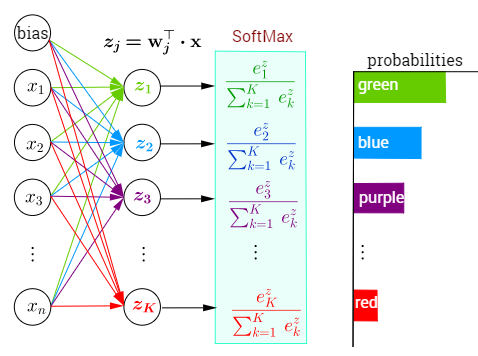
- 现在我们将优化参数以最大化观测数据的概率。
- 为了得到预测结果,我们将设置一个阈值,如选择具有最大概率的标签。
- 我们希望模型的输出\(\hat{y}_j\)可以视为属于类\(j\)的概率,然后选择具有最大输出值的类别\(\operatorname*{argmax}_j y_j\)作为我们的预测。
- 例如,如果\(\hat{y}_1\)、\(\hat{y}_2\)和\(\hat{y}_3\)分别为0.1、0.8和0.1,那么我们预测的类别是2,在我们的例子中代表“鸡”。
- 社会科学家邓肯·卢斯于1959年在选择模型(choice model)的理论基础上发明的softmax函数 如下式:
交叉熵损失函数
- 一般用于分类问题 \(H(p, q)=-\sum_{x} p(x) \log q(x)\)
- 交叉熵刻画的是两个概率分布之间的距离, p代表正确答案, q代表的是预测值,交叉熵越小,两个概率的分布约接近
举例
- 假设有一个3分类问题,某个样例的正确答案是(1, 0, 0)
- 甲模型经过softmax回归之后的预测答案是(0.5, 0.2, 0.3)
- 乙模型经过softmax回归之后的预测答案是(0.7, 0.1, 0.2)
import torch
def softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition # 这里应用了广播机制
X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
def cross_entropy(y_hat, y):
return - torch.log(y_hat[range(len(y_hat)), y])
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
X_prob, X_prob.sum(1),y_hat[[0, 1], y],cross_entropy(y_hat, y)
(tensor([[0.0369, 0.0550, 0.0587, 0.5402, 0.3092],
[0.2373, 0.6351, 0.0845, 0.0074, 0.0357]]),
tensor([1.0000, 1.0000]),
tensor([0.1000, 0.5000]),
tensor([2.3026, 0.6931]))
卷积神经网络
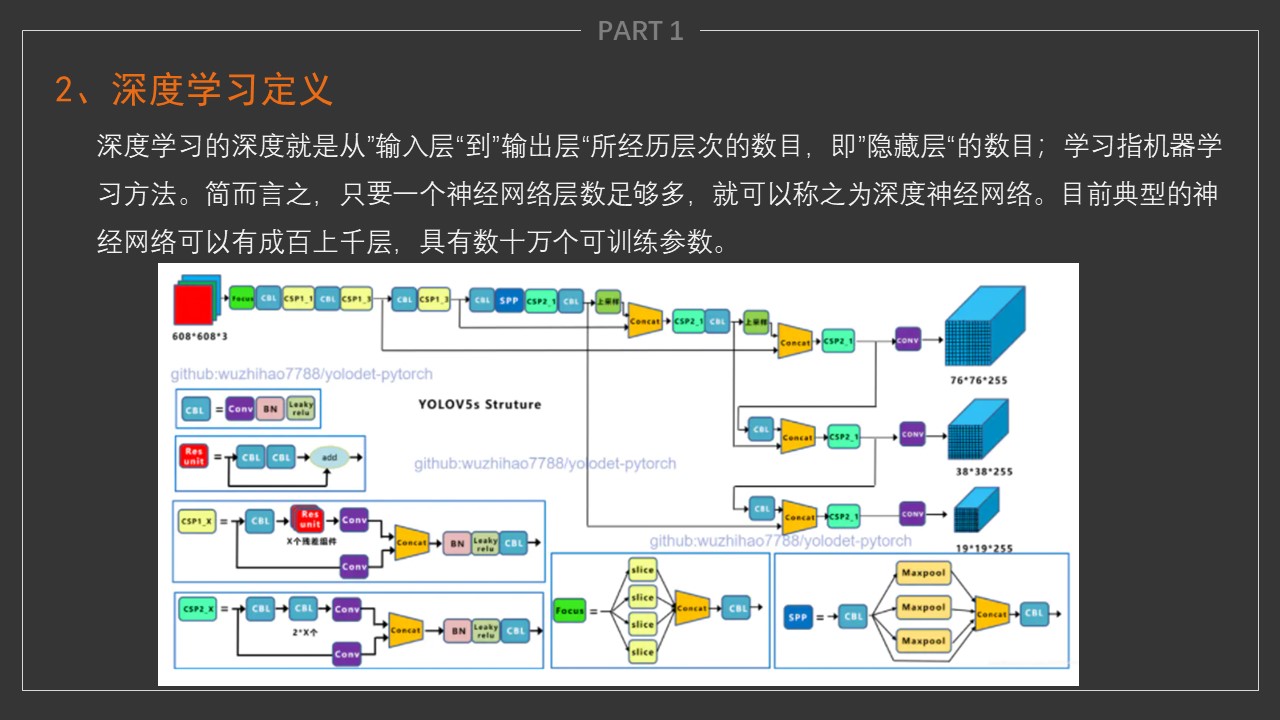
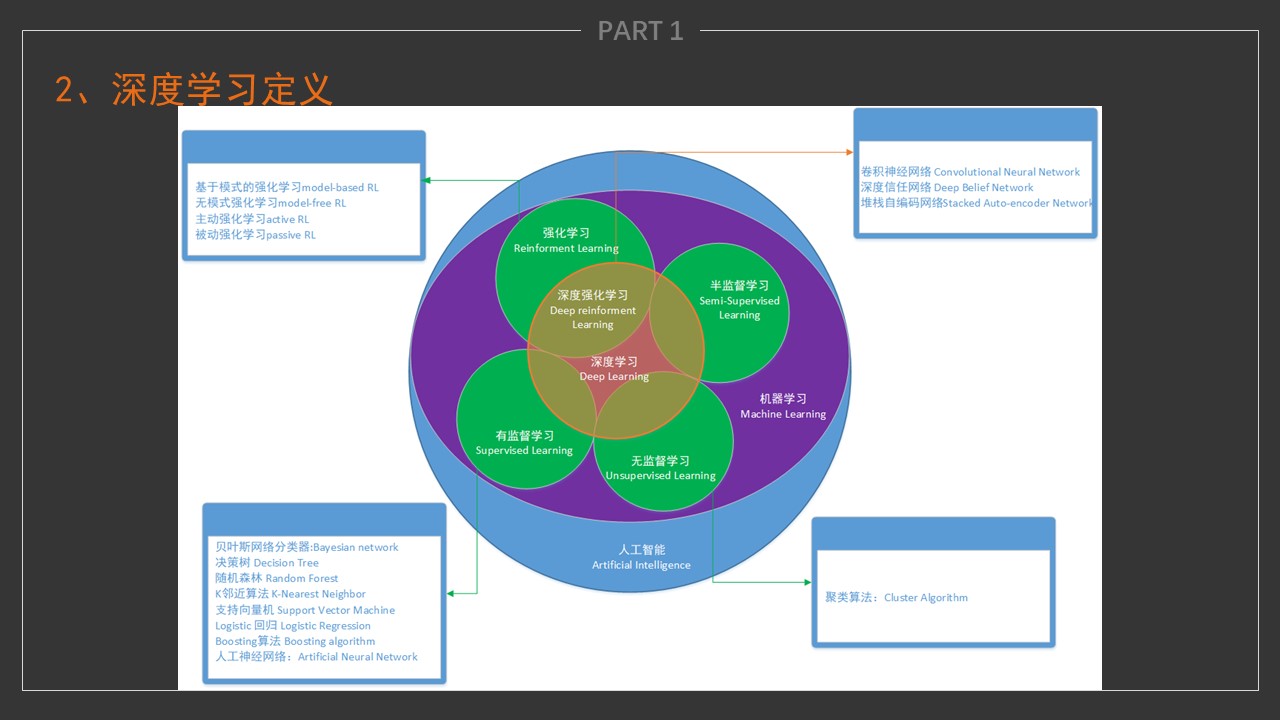
- 深度学习是指多层神经网络上运用各种机器学习算法解决图像,文本等各种问题的算法集合。
- 深度学习的核心是特征学习,旨在通过分层网络获取分层次的特征信息,从而解决以往需要人工设计特征的重要难题。
- 人类的视觉原理如下:
- 从原始信号摄入开始(瞳孔摄入像素 Pixels)
- 接着做初步处理(大脑皮层某些细胞发现边缘和方向)
- 然后抽象(大脑判定,眼前的物体的形状,是圆形的)
- 然后进一步抽象(大脑进一步判定该物体是只气球)。

概念
- 卷积神经网络是一种多层神经网络,擅长处理图像特别是大图像的相关机器学习问题。CNN通过卷积来模拟特征区分,并且通过卷积的权值共享及池化,来降低网络参数的数量级,最后通过传统神经网络完成分类等任务。
- 卷积神经网络是一种自动化特征提取的机器学习模型,主要用于解决图像识别问题。
- 从直观上讲,是一个从细节到抽象的过程。这里的关键是如何抽象,抽象就是把图像中的各种零散的特征通过某种方式汇总起来,形成新的特征。深度学习网络最上层的特征是最抽象的。
降低网络参数数量级
- 神经网络结构 : 在该结构中, 输入是一个向量,然后在一系列的隐层中对它做变换, 如果一个尺寸为200x200x3的图像,采用全连接方式会让每个神经元包含200x200x3=120,000个权重值, 这种全连接方式效率低下,大量的参数也很快会导致网络过拟合。
卷积层:整合输入数据并从中提取有效数据,得到特征图。
- 在这个卷积层,有两个关键操作:局部关联与窗口滑动。局部关联将每个神经元看作一个滤波器,窗口滑动则是使用滤波器对局部数据计算。
- 局部感知:人的大脑识别图片的过程中,并不是一下子整张图同时识别,而是对于图片中的每一个特征首先局部感知,然后更高层次对局部进行综合操作,从而得到全局信息。
- 卷积运算一个重要的特点就是,通过卷积运算,可以使原信号特征增强,并且降低噪音
- 这个过程我们可以理解为我们使用一个过滤器(卷积核)来过滤图像的各个小区域,从而得到这些小区域的特征值。
- 在实际训练过程中,卷积核的值是在学习过程中学到的。
- 使用多个滤波器,可以通过卷积将一维的输入变为四维,每一维代表一个特征。
- 每个卷积核的大小都是3维(x * y * n),代表长、宽和输入的深度,而其本身的深度是指卷积核个数,设为 k ,则该层卷积核参数个数为(x * y * n * k)
池化层(降采样层):池化层能够压缩数据,提取明显特征。
- 池化层位于连续的卷积层中间,本身没有可训练的参数。池化层的目的在于对卷积层提取的特征进行降维,减少整个神经网络的参数。
- 感受野:一个像素对应回原图的区域大小,假如没有pooling,一个\(3*3\),步长为1的卷积,那么输出的一个像素的感受野就是\(3*3\)的区域,再加一个stride=1的\(3*3\)卷积,则感受野为\(5*5\)。
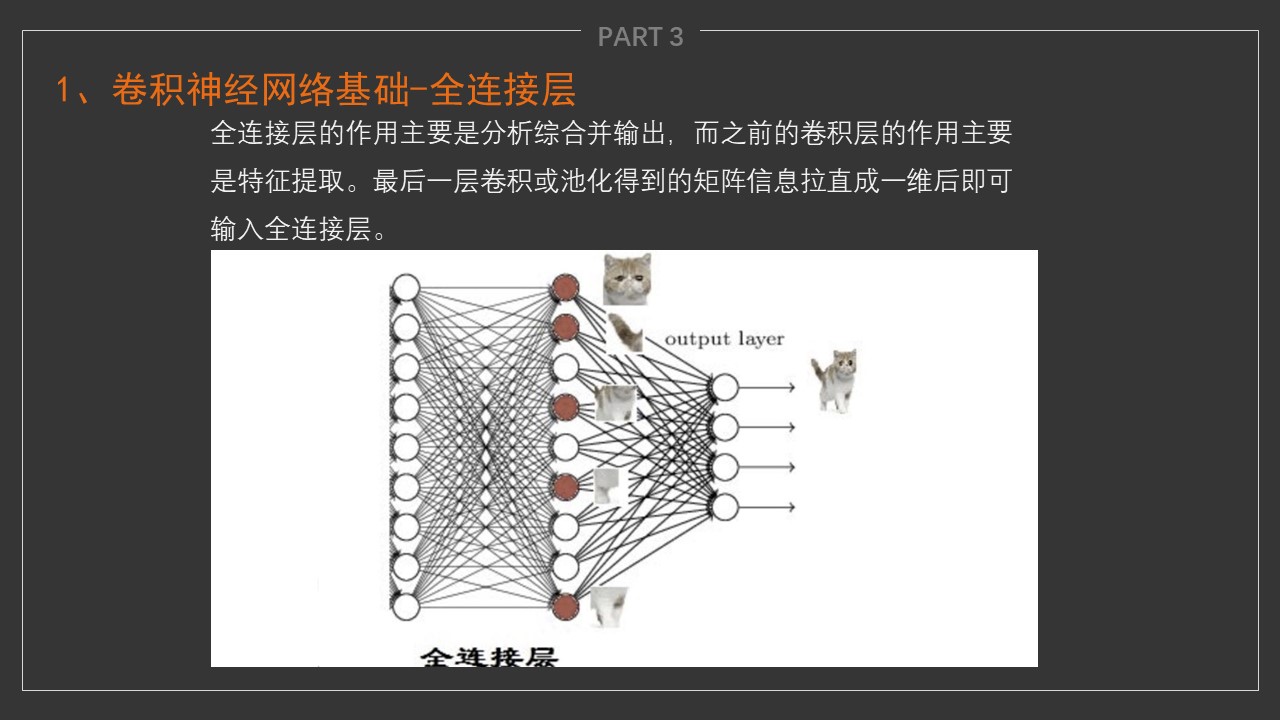
全连接层:将两层之间所有神经元都有权重连接。
- 全连接层将两层之间所有神经元都有权重连接,通常全连接层在卷积神经网络尾部,与传统的神经网络神经元的连接方式是一样的。
- 经过几轮卷积和池化操作,可以认为图像中的信息已经被抽象成了信息含量更高的特征。我们可以将卷积和池化看成自动图像提取的过程,在特征提取完成后,仍然需要使用全连接层来完成分类任务
实用举例
!pip install torchsummary
Requirement already satisfied: torchsummary in d:\miniconda3\lib\site-packages (1.5.1)
引入需要的库
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import time
import torch.optim as optim
import torchvision
import torch.utils.data as Data
import torchvision.transforms as transforms
from torchvision.datasets import MNIST,FashionMNIST
print('GPU useable state: ',torch.cuda.is_available())
GPU useable state: False
加载数据
transform = transforms.Compose(
[transforms.ToTensor()])
# transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# MNIST
data_train = MNIST(root = "data/", ## 数据的路径,如果存在数据则加载,否则下载至此路径
transform = transform, ## 图像变换操作
train =True, ## 决定使用训练集还是测试集
download = True) ## 选择是否需要下载数据
data_test = MNIST(root = "data/",
transform = transform,
train =False)
## 定义数据加载器
batch_size = 256
train_loader = Data.DataLoader(dataset = data_train, ## 使用的数据集
batch_size = batch_size, ## 批处理样本大小
shuffle = True ## 是否打乱数据顺序
)
test_loader = Data.DataLoader(dataset = data_test,
batch_size = batch_size,
shuffle = True #将顺序随机打乱
)
定义网络模型
卷积神经网络模型
class ConvNet(nn.Module):
def __init__(self, ch = 3, h = 32, w = 32):
super(ConvNet, self).__init__()
# 3 input image channel, 6 https://haodong-li.com/zju/assets/img/vision_2022/6/output channels, 5x5 square convolution
# kernel
self.conv1 = nn.Sequential(
nn.Conv2d(
in_channels = ch,
out_channels = 6,
kernel_size = 5), ## (N*1* h * w ) ==> (N*6* (h-4) * (w-4))
nn.ReLU(),
nn.AvgPool2d(
kernel_size = 2,
stride = 2) ## (N*6* (h-4) * (w-4)) ==> (N*6* (w-4)/2 * (w-4)/2)
)
self.conv2 = nn.Sequential(
nn.Conv2d(6, 16, 5), ## (N*6* (h-4)/2 * (w-4)/2) ==> (N*16* (h-4)/2-4 * (w-4)/2-4)
nn.ReLU(),
nn.AvgPool2d(2,2) ## (N*16* (h-4)/2-4 * (w-4)/2-4) ==> (N*16* h/4 -3 * w/4 -3)
)
self.classifier = nn.Sequential(
nn.Linear(int(16*(h/4-3)*(w/4-3)),120), # 5
nn.ReLU(),
nn.Linear(120,84),
nn.ReLU(),
nn.Linear(84,10))
def forward(self, x):
# Max pooling over a (2, 2) window
x = self.conv1(x)
# If the size is a square, you can specify with a single number
x = self.conv2(x)
x = torch.flatten(x, 1) # flatten all dimensions except the batch dimension
x = self.classifier(x)
return x
MLP(多层感知机、全连接网络)
class dnn(nn.Module):
def __init__(self):
super(dnn,self).__init__()
## 定义层
self.flatten = nn.Flatten()
self.hiden1 = nn.Linear(in_features = 784, out_features = 512, bias = True)
self.active1 = nn.ReLU() ## 激活函数
self.drop1 = nn.Dropout(p=0.2)
self.hiden2 = nn.Linear(512,512)
self.active2 = nn.ReLU()
self.drop2 = nn.Dropout(p=0.2)
self.fc = nn.Linear(512,10)
def forward(self,x):
x = self.flatten(x)
x = self.hiden1(x)
x = self.active1(x)
x = self.drop1(x)
x = self.hiden2(x)
x = self.active2(x)
x = self.drop2(x)
x = self.fc(x)
return x
实例化网络模型
net = dnn()
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
net.to(device)
print(device)
from torchsummary import summary
summary(net,(1,28,28))
cpu
----------------------------------------------------------------
Layer (type) https://haodong-li.com/zju/assets/img/vision_2022/6/output Shape Param #
================================================================
Flatten-1 [-1, 784] 0
Linear-2 [-1, 512] 401,920
ReLU-3 [-1, 512] 0
Dropout-4 [-1, 512] 0
Linear-5 [-1, 512] 262,656
ReLU-6 [-1, 512] 0
Dropout-7 [-1, 512] 0
Linear-8 [-1, 10] 5,130
================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.03
Params size (MB): 2.55
Estimated Total Size (MB): 2.59
----------------------------------------------------------------
net = ConvNet(1,28,28)
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
net.to(device)
print(device)
from torchsummary import summary
summary(net,(1,28,28))
cpu
----------------------------------------------------------------
Layer (type) https://haodong-li.com/zju/assets/img/vision_2022/6/output Shape Param #
================================================================
Conv2d-1 [-1, 6, 24, 24] 156
ReLU-2 [-1, 6, 24, 24] 0
AvgPool2d-3 [-1, 6, 12, 12] 0
Conv2d-4 [-1, 16, 8, 8] 2,416
ReLU-5 [-1, 16, 8, 8] 0
AvgPool2d-6 [-1, 16, 4, 4] 0
Linear-7 [-1, 120] 30,840
ReLU-8 [-1, 120] 0
Linear-9 [-1, 84] 10,164
ReLU-10 [-1, 84] 0
Linear-11 [-1, 10] 850
================================================================
Total params: 44,426
Trainable params: 44,426
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.08
Params size (MB): 0.17
Estimated Total Size (MB): 0.25
----------------------------------------------------------------
## 初始化模型参数
def init_weights(m):
if type(m) == nn.Conv2d:
nn.init.normal_(m.weight, mean=0, std=0.5)
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
定义模型训练函数
import pandas as pd
def train_model(model, train_loader, test_loader, loss_func, optimizer, device, num_epochs = 5):
"""
model: 网络模型; train_loader: 训练数据集; test_loader: 测试数据集
loss_func: 损失函数; optimizer: 优化方法; num_epochs: 训练的轮数
device: 控制是否使用GPU
"""
train_loss_all = []
train_acc_all = []
val_acc_all = []
val_loss_all = []
gap = len(train_loader)//30
start_time = time.time()
for epoch in range(num_epochs):
if epoch:
print('-'*10)
print("Epoch {}/{}".format(epoch + 1,num_epochs))
##
train_loss = 0.0
train_corrects = 0
train_num = 0
val_loss = 0.0
val_corrects = 0
val_num = 0
for step,data in enumerate(train_loader):
model.train()
x,y = data[0].to(device), data[1].to(device)
output = model(x) ## 模型在 X 上的输出: N * num_class
pre_lab = torch.argmax(output, 1) ## 获得预测结果
loss = loss_func(output, y) ## 损失
optimizer.zero_grad() ## 每次迭代将梯度初始化为0
loss.backward() ## 损失的后向传播, 计算梯度
optimizer.step() ## 使用梯度进行优化
train_loss += loss.item() * x.size(0) ## 统计模型预测损失
train_corrects += torch.sum(pre_lab == y.data)
train_num += x.size(0)
if step %gap == gap-1:
cont = step//gap
if cont >30:
cont = 30
print(str(cont)+'/','30','['+'='*cont+'>'+'-'*(30-cont)+']',
'loss: {:.4f} - accuracy: {:.4f}'.format(train_loss/train_num,train_corrects.double().item()/train_num)
,end="\r")
for data in test_loader:
model.eval()
X_test, y_test = data[0].to(device), data[1].to(device)
X_test.requires_grad=True
with torch.no_grad():
output = model(X_test)
test_loss = loss_func(output, y_test )
_, pred = torch.max(output.data, 1)
val_corrects += torch.sum(pred == y_test.data)
val_loss += test_loss.item()*X_test.size(0)
val_num += X_test.size(0)
##
train_loss_all.append(train_loss/train_num)
train_acc_all.append(train_corrects.double().item()/train_num)
val_loss_all.append(val_loss/val_num)
val_acc_all.append(val_corrects.double().item()/val_num)
print('')
print("No.{} Train Loss is:{:.4f}, Train_accuracy is {:.4f}%"
.format(epoch+1, train_loss_all[-1],train_acc_all[-1] * 100))
print("No.{} Val Loss is:{:.4f}, Val_accuracy is {:.4f}%"
.format(epoch+1, val_loss_all[-1], val_acc_all[-1] * 100))
time_use = time.time() - start_time
print("Train and val complete in {:.0f}m {:.0f}s".format(time_use//60, time_use%60))
train_process = pd.DataFrame(
data = {"epoch":range(num_epochs),
"train_loss":train_loss_all,
"train_acc":train_acc_all,
"val_loss":val_loss_all,
"val_acc":val_acc_all})
return model, train_process
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
net, train_process = train_model(net, train_loader, test_loader, criterion, optimizer, device, num_epochs = 10)
Epoch 1/10
30/ 30 [==============================>] loss: 2.3930 - accuracy: 0.1195
No.1 Train Loss is:2.3918, Train_accuracy is 11.9200%
No.1 Val Loss is:2.3016, Val_accuracy is 11.3500%
Train and val complete in 0m 7s
----------
Epoch 2/10
30/ 30 [==============================>] loss: 2.3022 - accuracy: 0.1095loss: 2.3022 - accuracy: 0.108730 [==============================>] loss: 2.3022 - accuracy: 0.1093
No.2 Train Loss is:2.3022, Train_accuracy is 10.9667%
No.2 Val Loss is:2.3020, Val_accuracy is 11.3500%
Train and val complete in 0m 14s
----------
Epoch 3/10
30/ 30 [==============================>] loss: 2.3022 - accuracy: 0.1111loss: 2.3022 - accuracy: 0.1100
No.3 Train Loss is:2.3022, Train_accuracy is 11.1017%
No.3 Val Loss is:2.3018, Val_accuracy is 11.3500%
Train and val complete in 0m 21s
----------
Epoch 4/10
30/ 30 [==============================>] loss: 2.3022 - accuracy: 0.1104
No.4 Train Loss is:2.3022, Train_accuracy is 11.0283%
No.4 Val Loss is:2.3019, Val_accuracy is 11.3500%
Train and val complete in 0m 28s
----------
Epoch 5/10
30/ 30 [==============================>] loss: 2.3021 - accuracy: 0.1113
No.5 Train Loss is:2.3022, Train_accuracy is 11.1300%
No.5 Val Loss is:2.3013, Val_accuracy is 11.3500%
Train and val complete in 0m 36s
----------
Epoch 6/10
30/ 30 [==============================>] loss: 2.3022 - accuracy: 0.11140 [======>------------------------] loss: 2.3017 - accuracy: 0.1146
No.6 Train Loss is:2.3022, Train_accuracy is 11.1350%
No.6 Val Loss is:2.3014, Val_accuracy is 11.3500%
Train and val complete in 0m 43s
----------
Epoch 7/10
30/ 30 [==============================>] loss: 2.3020 - accuracy: 0.1113
No.7 Train Loss is:2.3020, Train_accuracy is 11.1183%
No.7 Val Loss is:2.3012, Val_accuracy is 11.3500%
Train and val complete in 0m 50s
----------
Epoch 8/10
30/ 30 [==============================>] loss: 2.3021 - accuracy: 0.1100 [=================>-------------] loss: 2.3019 - accuracy: 0.1109
No.8 Train Loss is:2.3021, Train_accuracy is 11.0117%
No.8 Val Loss is:2.3028, Val_accuracy is 11.3500%
Train and val complete in 0m 57s
----------
Epoch 9/10
30/ 30 [==============================>] loss: 2.3025 - accuracy: 0.1090
No.9 Train Loss is:2.3025, Train_accuracy is 10.9283%
No.9 Val Loss is:2.3012, Val_accuracy is 11.3500%
Train and val complete in 1m 5s
----------
Epoch 10/10
30/ 30 [==============================>] loss: 2.3022 - accuracy: 0.1100
No.10 Train Loss is:2.3022, Train_accuracy is 10.9983%
No.10 Val Loss is:2.3014, Val_accuracy is 11.3500%
Train and val complete in 1m 14s
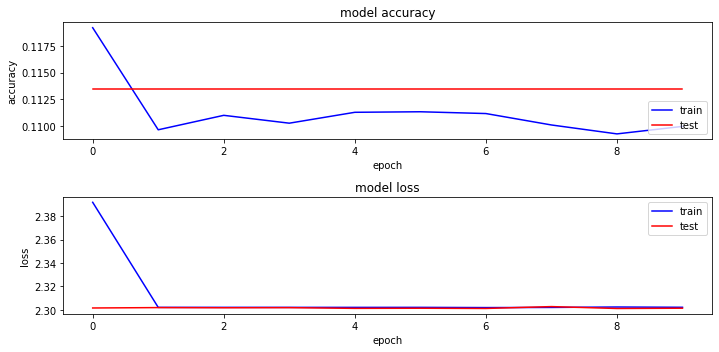
# plotting the metrics
fig = plt.figure(figsize=(10,5))
plt.subplot(2,1,1)
plt.plot(train_process.train_acc, "b-")
plt.plot(train_process.val_acc, "r-")
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='lower right')
plt.subplot(2,1,2)
plt.plot(train_process.train_loss, "b-")
plt.plot(train_process.val_loss, "r-")
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
# plt.legend(['train'], loc='upper right')
plt.legend(['train', 'test'], loc='upper right')
plt.tight_layout()
for x,y in test_loader:
break
plt.imshow(x[0].squeeze().numpy(),'gray')
<matplotlib.image.AxesImage at 0x1c3128927f0>
output = net.conv1(x[0].unsqueeze(dim=0).to(device))
for i in range(6):
plt.subplot(2,3,i+1)
plt.imshow(output[0][i].squeeze().detach().cpu().numpy(),'gray')